4
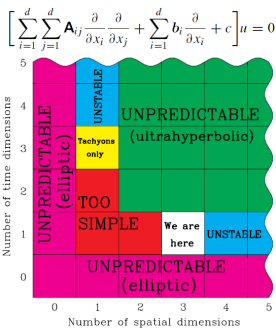
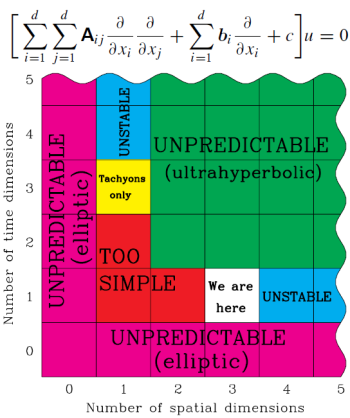
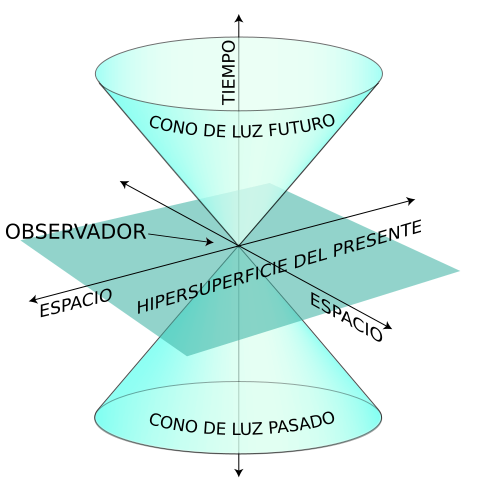
La propagación de ondas solo puede estar descrita por ecuaciones covariantes hiperbólicas (las elípticas no lo permiten y las ultrahiperbólicas están mal puestas). Además, si requerimos que el espaciotiempo tenga una complejidad mínima para permitir la existencia de seres conscientes, tenga un futuro que sea predecible y permita la existencia de movimientos orbitales estables, necesariamente debe tener tres dimensiones espaciales y una temporal, espaciotiempo 3+1.